Elemental Probability
June 2025
Late last year I began exploring a new collectible card game called Sorcery: Contested Realm. There are two primary resources needed to play cards in the game: mana and threshold. Threshold is a mechanic which counts the number of elemental attributes of Site cards on your board. Spell cards may require a certain amount of threshold present to be played. Browse, for example, costs 1 mana but requires 3 Air threshold.
In March of 2025 I wanted to modify the deck I'd been using at weekly Sorcery events by adding a third element. The more elements to balance in a deck, the less consistent it will perform. My deck wanted to have a particular threshold amount by turn four. I intuitively made changes to the Site deck, but a question lingered:
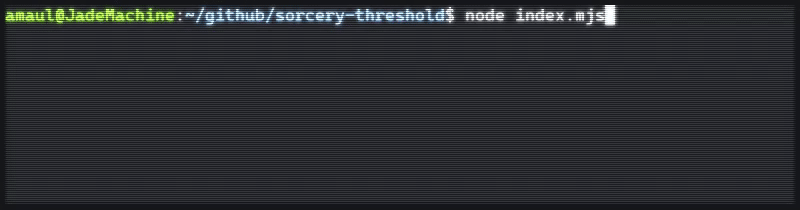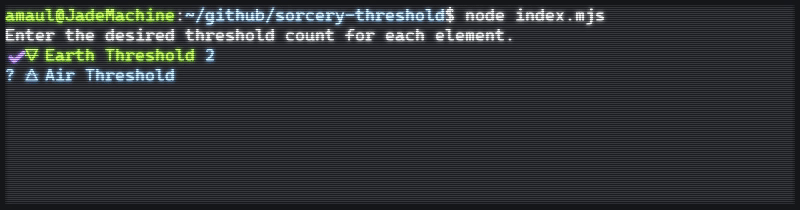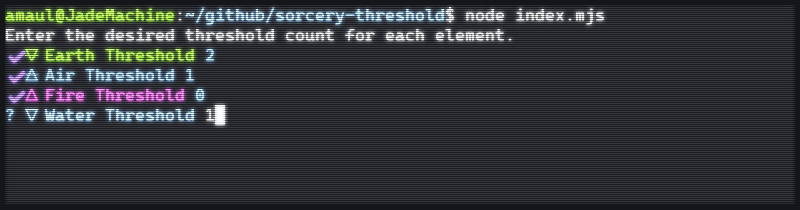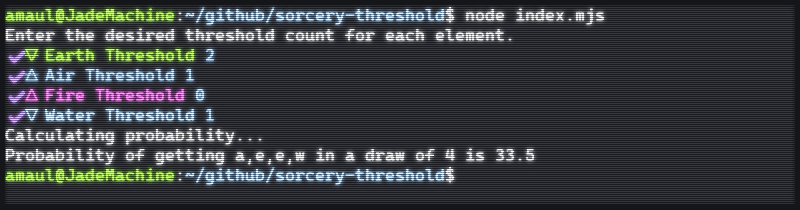
What was the actual probability I would get Air, Earth, Earth, Water threshold on turn four?
The App
 The finished product
The finished product
The culmination of work started by that question came to be a Node app. It prompts the user with the type of criteria needed, and parses a user-provided text list using a downloaded dump of Sorcery card data. There are flags for different options: calculation vs simulation, additional card draws, etc.
This project required that I learn about multivariate hypergeometric distributions, Monte Carlo method simulations, and more.
Oh and that original question? Turns out the probability of my deck getting the perfect threshold on turn four is ~33%. A single mulligan brings that to 62%, tossing two Sites increases it to 78%, and a full mulligan of the site hand is roughly 87%.
This project was a fun adventure, and my Sorcery decks have a stronger showing because of it. Feel free to check it out on Github.


